The problem of estimation the maximum possible magnitude of regional earthquakes Mmax is examined. Statistical and paleoseismological approaches to this problem are combined. Within the framework of the statistical approach, the method of statistical moments, the Bayes method, the method based on the theory of extreme values (EVT) are examined and compared.
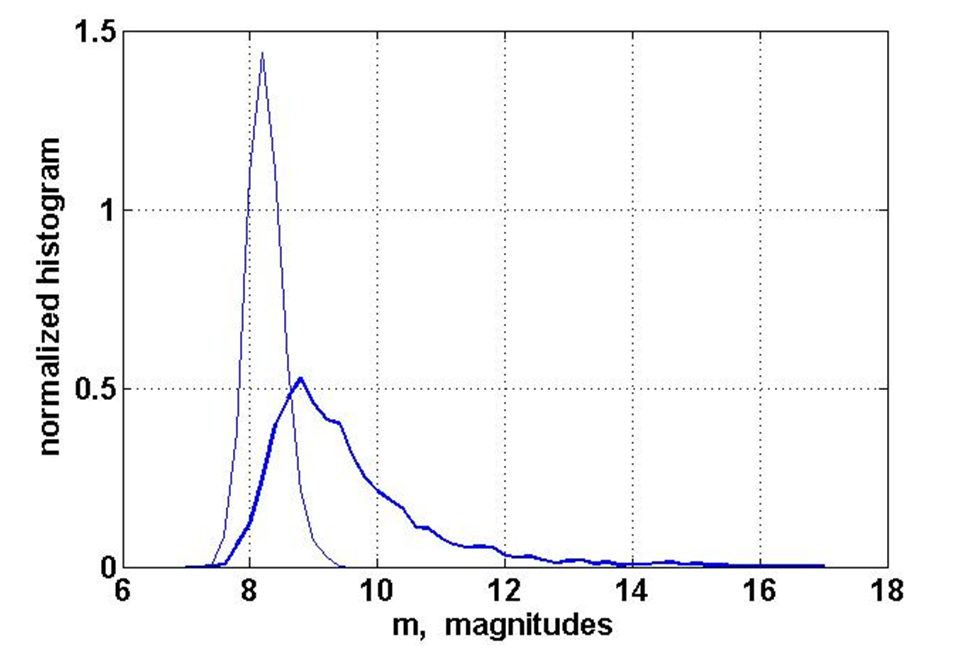
A comparison of Mmax estimates within the framework of the truncated Gutenberg-Riecher law and from the EVT method was carried out. As a stable alternative to the potentially non-robust Mmax values, the quantiles Qq(T) of the maximum earthquake in the future time horizon T with probability q are suggested (see Fig.). The use of quantiles allow to choose the time horizon T and the level of confidence q mostly suitable for the given problem of estimating the maximum possible magnitude of an earthquake. The convenient in practiceconnection between the quantiles of a single event and the maximum event in the future time interval T has been established. A few mostly representative paleoseismological studies were analyzed, and as a result of the analysis the evidence of possibility of earthquakes with a magnitude significantly exceeding the Mmax value obtained for the truncated Gutenberg-Richter law has been revealed.
Pisarenko, V.F., Rodkin, M.V. Approaches to Solving the Maximum Possible Earthquake Magnitude ( M max ) Problem. SurvGeophys (2022). DOI:

