The paper titled “Phaseless inverse scattering with background information” was published in “Inverse Problems” (Q1 WoS) journal. Doctor of Physical and Mathematical sciences, Senior Researcher of IEPT RAS Novikov R.G. is one of coauthors.
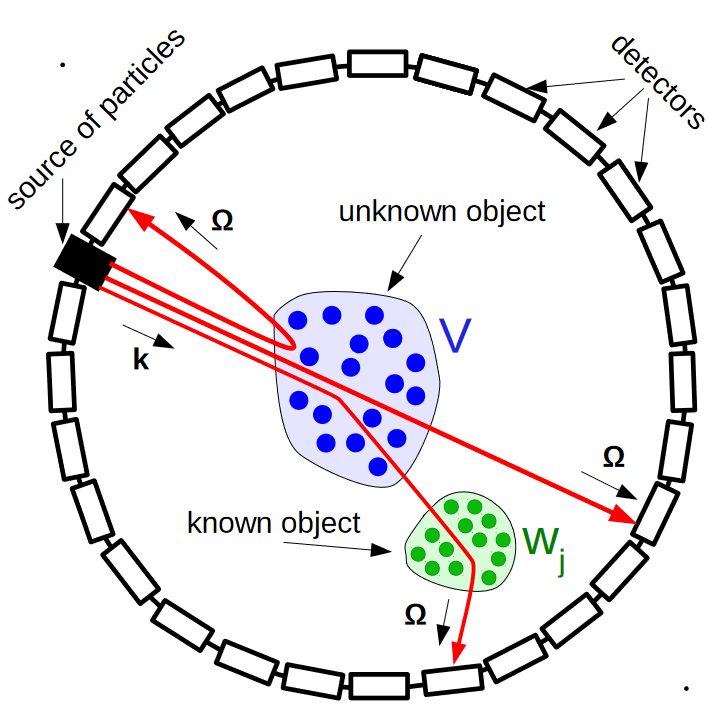
The work deals with phaseless inverse scattering for the multidimensional Schrödinger equation with unknown potential v using the method of known background scatterers.
In particular, in dimension d ⩾ 2, the authors show that |f1|2 at high energies uniquely determines v via explicit formulas, where f1 is the scattering amplitude for v + w1, where w1 is an a priori known nonzero background scatterer, under the condition that supp v and supp w1 are sufficiently disjoint.
If this condition is relaxed, then the authors give similar formulas for finding v from |f|2, |f1|2, where f is the scattering amplitude for v.
Results of the work are new even in the Born approximation when f1 and f reduce to Fourier transforms of v + w1 and v (respectively).
In particular, the authors continue studies of Novikov (2016 J. Geom. Anal., 26, 346 – 359) and Leshem et al (2016, Nat. Commun., 7, 1–6).
Source: R.G. Novikov, V.N. Sivkin, Phaseless inverse scattering with background information // Inverse Problems. 2021. V. 37. № 5. Article 055011(20pp) DOI: 10.1088/1361-6420/abf36c