In the journal “Zeitschrift für angewandte Mathematik und Physik” (WoS, Scopus, Q1) publishedby Springer, the article“A boundary value problem in the theory of elasticity for a rectangle: exact solutions” was published. Among the authorsareemployees of IEPT RAS: Leading Researcher, D.Sc. (Phys.-Math.) M.D. Kovalenko, Senior Researcher, Cand. Sc. (Phys.-Math.) I.V. MenshovaandSenior Researcher, Cand. Sc. (Phys.-Math.) A.P. Kerzhaev.
In the article, we derive the formulas that describe the exact solution of the boundary value problem in the theory of elasticity for a rectangle in which two opposite (horizontal) sides are free and stresses are specified (all cases of symmetry relative to the central axes) on the other two sides (rectangle ends). The formulas for a half-strip are also given. The solutions are represented as series in Papkovich–Fadle eigenfunctions whose coefficients are determined from simple formulas.
The research was funded by RFBR and NSFC according to the research project No. 20-51-53021 and the Russian Science Foundation under grant No. 19-71-00094.
The exact solution of the boundary value problem in a rectangle with specific boundary conditions on its sides is, perhaps, one of the best-known problems in the theory of elasticity for many decades. Hundreds of publications are devoted to it. The interest in this problem stems primarily from theoretical questions, such as the influence of end effects, the behavior of solutions in the neighborhood of a boundary’s corner points (for example, can the solution for an infinite wedge be considered as an asymptotic one in the corresponding problems for a rectangle?), the assessment of various approximate theories (in particular, the beam one), etc. The solution of the problem for a rectangle opens the way to solving important applied problems: the transfer of concentrated loads to a thin sheet through stiffening ribs, inhomogeneous and temperature problems, problems with cracks in a rectangular region, and so on. The development of analogous theories in oblique and polar coordinate systems would allow a lot of other problems (homogeneous, inhomogeneous, temperature ones) to be solved. In the oblique coordinate system these are the solutions for a trapezium, a triangle, a rectangle with an oblique “crack”, etc. In the polar coordinate system these are the solutions for part of a ring, a half-plane with circular recesses or holes, etc. Finally, the solution for a rectangle underlies the exact solution of the classical three-dimensional boundary value problem in the theory of elasticity for a rectangular parallelepiped.
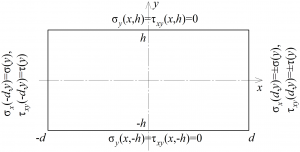The importance of exact solutions can hardly be overestimated. This is mostly due to the fact that they allow us to deeply understand the physics of the phenomenon under study, to answer the question of the adequacy of the mathematical model used to the investigated physical phenomenon, to evaluate the effectiveness of the use of certain approximate or numerical methods in solving complex engineering problems.
This paper is based on the theory of expansions in terms of Papkovich–Fadle eigenfunctions and the Borel transform in the class of quasi-entire functions of exponential type with a domain of analyticity degenerated into a segment (rectangle ends).
Strictly speaking, the derived formulas describe the residual stresses and those displacements that result from their release with the formation of discontinuities. Therefore, our analysis is conducted from the perspective of residual stresses. In order to pass to the solutions in the classical formulation, the signs in the formulas for the displacements or stresses need to be reversed in a certain way.
All our formulas are derived by assuming that the discontinuities of the displacements that arise when the residual stresses are released are known at the joints between the half-strips or rectangles glued together into an infinite strip with residual stresses. If, alternatively, the stresses are known, then we need to use the corresponding transition formulas relating the Lagrange coefficients for the displacements and stresses.
Source: Kovalenko M.D., Menshova I.V., Kerzhaev A.P., Yu G. A boundary value problem in the theory of elasticity for a rectangle: exact solutions. Z. Angew. Math.Phys., 2020, 71(6), 199. DOI: 10.1007/s00033-020-01425-2.
