The 11-years solar cycle is the most persistent periodicity observed in solar and geomagnetic indices. The origin of the solar cycle is related with the solar dynamo. Solar meridional circulation is believed to be responsible for the length of solar cycle and therefore be important for the solar cycle prediction. Recent advances in helioseismology provide a reconstruction of the meridional circulation profile during 23-24 solar cycles, which appears to be more complicated and variable than it was expected. The variability of the meridional circulation in time and space cause a discussion concerning the reliability of helioseismic reconstructions (Gizon, et al. 2020) and a true structure of the meridional circulation. We consider the solar cycle to be an evidence of a stable synchronization of the meridional circulation cells and apply the Kuramoto model of nonlinearly coupled oscillators as a model if the phase evolution of solar proxies.
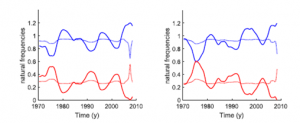
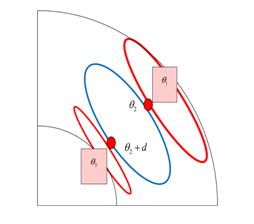
The present model consists of three non-identical oscillators coupled as a chain. Solar proxies provide observations of the phase evolution if the top and bottom oscillators (with respect to the solar surface), the middle oscillator is unobservable (Fig. 1). We suggest that there is a phase lag between the two points where the middle cell interacts with the top and the bottom circulation cells (Fig. 1) . Due to the phase lag this simple model acquires properties of more sophisticated Kuramoto models with conformist and contrarian oscillators. We determine a parametric area of stable synchronization relating the coupling coefficient and a phase lag. The model allows to reconstruct the evolution of natural frequencies of the near surface and the deep circulation cells for given parameters. It is demonstrated that high variability of the meridional circulation near the solar surface corresponds to maximal coupling and minimal phase lag of the parametric area of stable synchronization (Fig. 2, solid line).