Создан метод вычисления решения уравнения Монжа-Ампера с контрастной правой частью.
В космологии считается, что после отделения фотонов от вещества через 380 тысяч лет после Большого Взрыва распределение вещества было равномерным с точностью порядка 10-5-10-6 от средней плотности. Этой флюктуации оказалось достаточно, чтобы под действием гравитации распределение вещества во Вселенной стало крайне неравномерным — таким, каким мы его наблюдаем. Поскольку гравитация — потенциальная сила, на пространственных масштабах, существенно бóльших размеров галактик, перемещение вещества описывается градиентом решения т.н. уравнения Монжа-Ампера: det(∂2u/∂xi∂xj) = r(x), где правая часть r — плотность вещества во Вселенной в нашу эпоху. Если всюду r>0, то для стандартных краевых условий данное уравнение имеет единственное решение, но эта теорема может нарушаться уже при r³0. Это приводит к вычислительным сложностям при большой величине параметра контраста задачи rmax/rmin (что характерно для задач астрофизики). Если r — пространственно-периодическая функция, то u = u’ + c|x|2, где u’ имеет такую же периодичность, c = <r>/2, а угловые скобки обозначают усреднение по ячейке периодичности.
Метод предполагает последовательное вычисление решений регуляризованных уравнений и их экстраполяцию по параметру регуляризации. Он был применен для модельного распределения вещества по трем «галактикам» в кубе периодичности [-1/2,1/2]3 с гауссовым распределением вещества каждой «галактики». Параметр контраста задачи ~107.
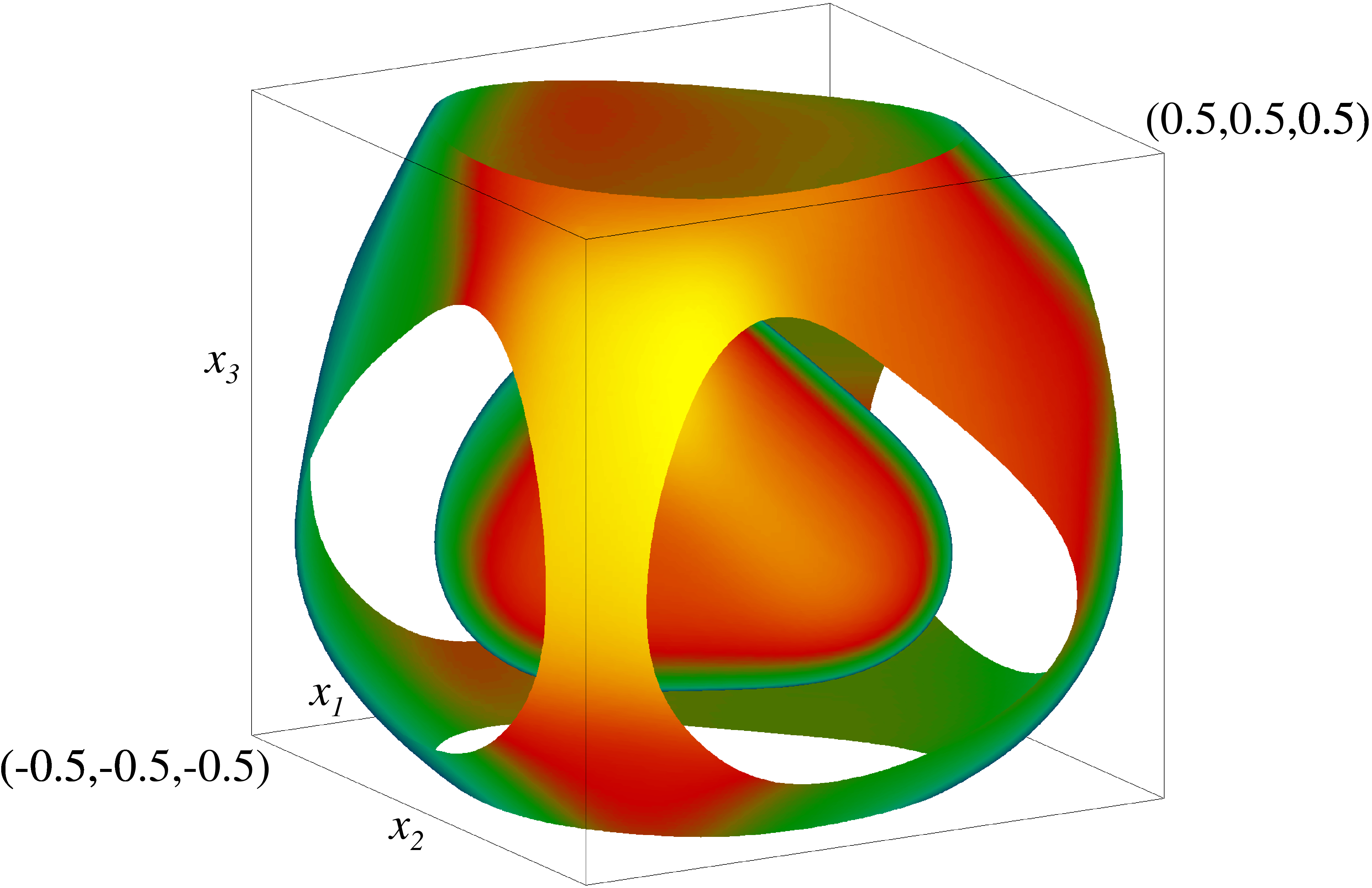
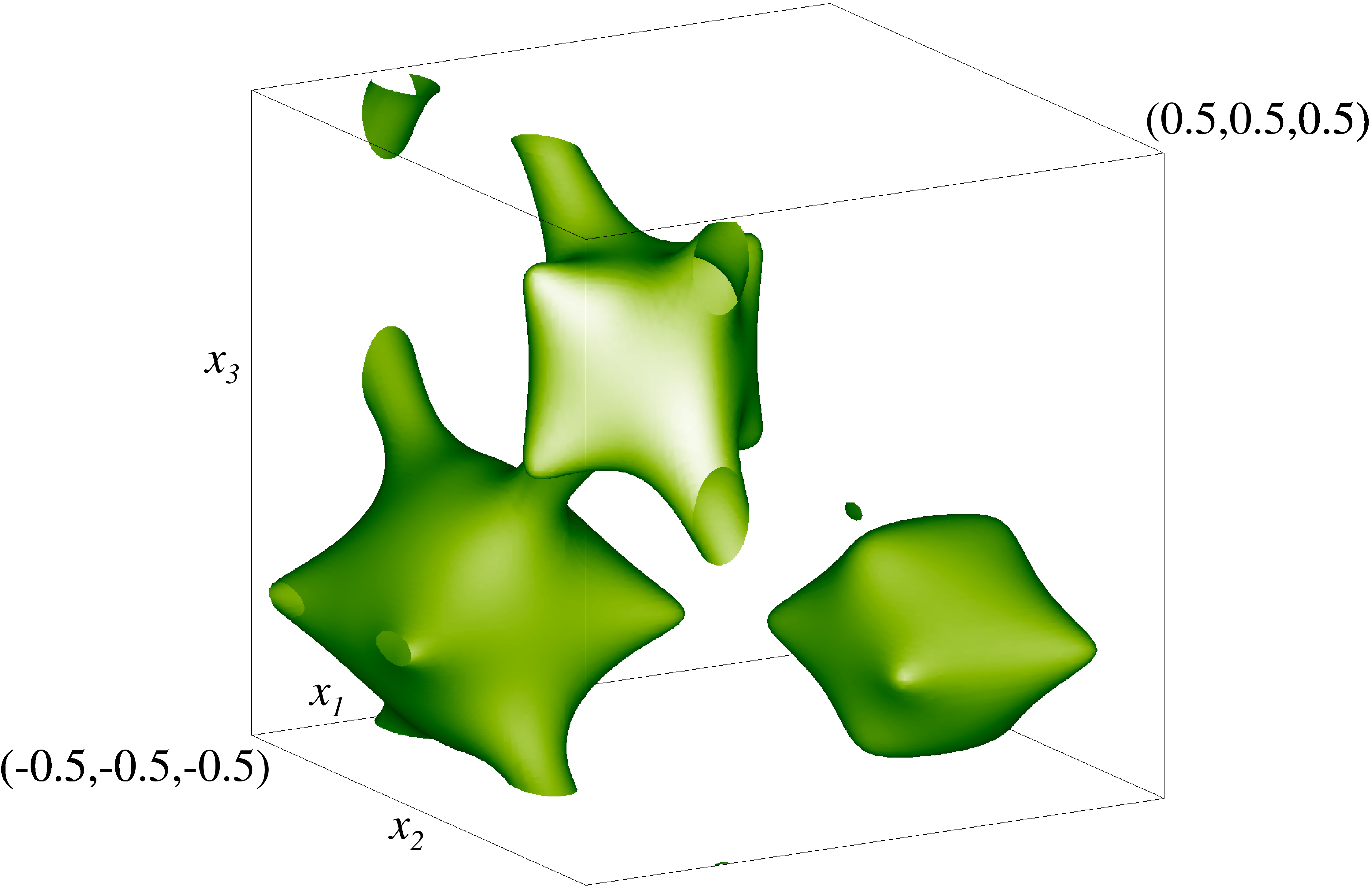
Слева: изоповерхности решения u для модельной задачи на уровнях 1/2 и 1/8 максимума u. Справа: изоповерхность Δu’ (лапласиана u’) на уровне 1/3 максимума. Модельные «галактики» находятся внутри показанных структур. Показан куб периодичности распределения r.
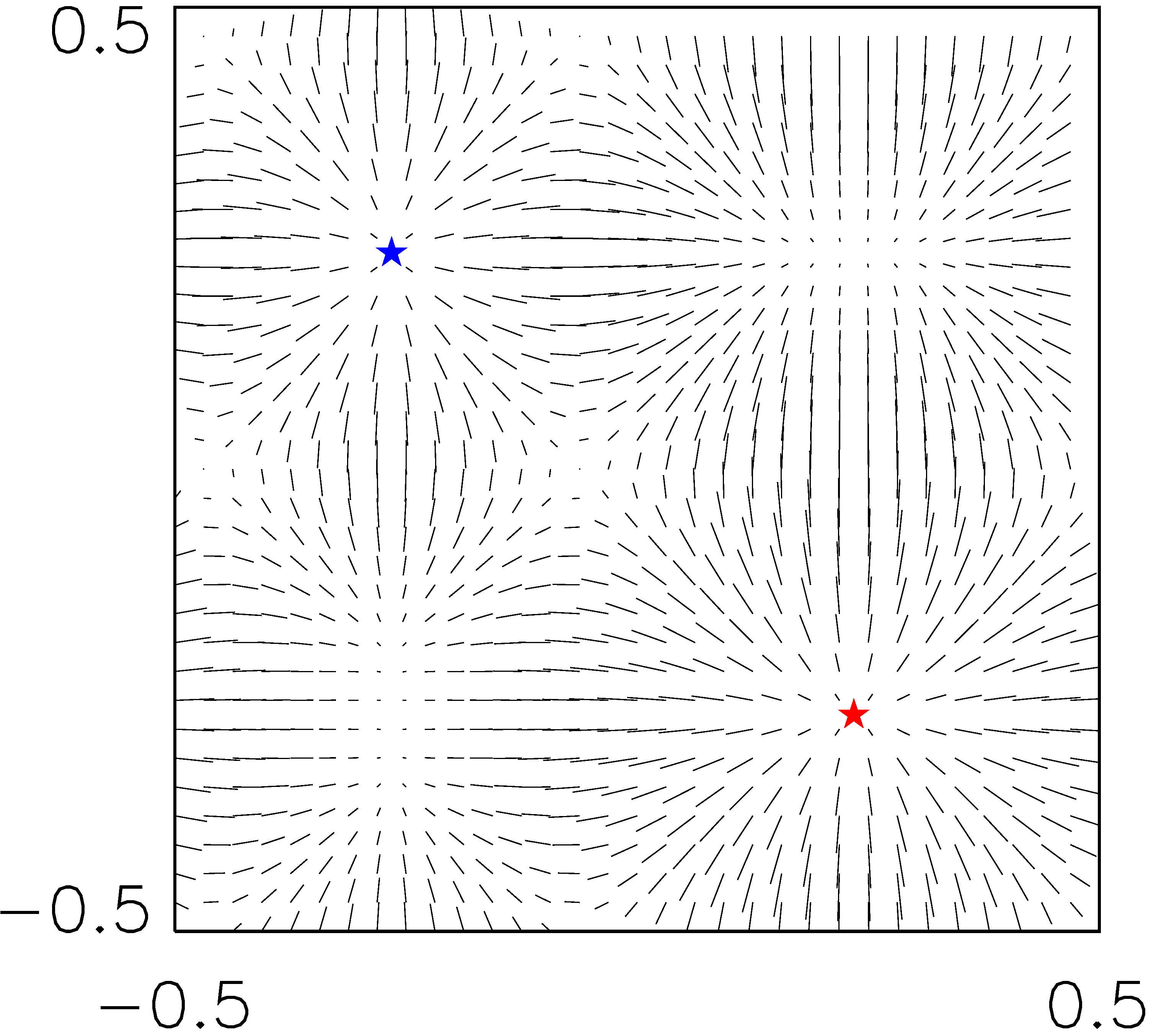
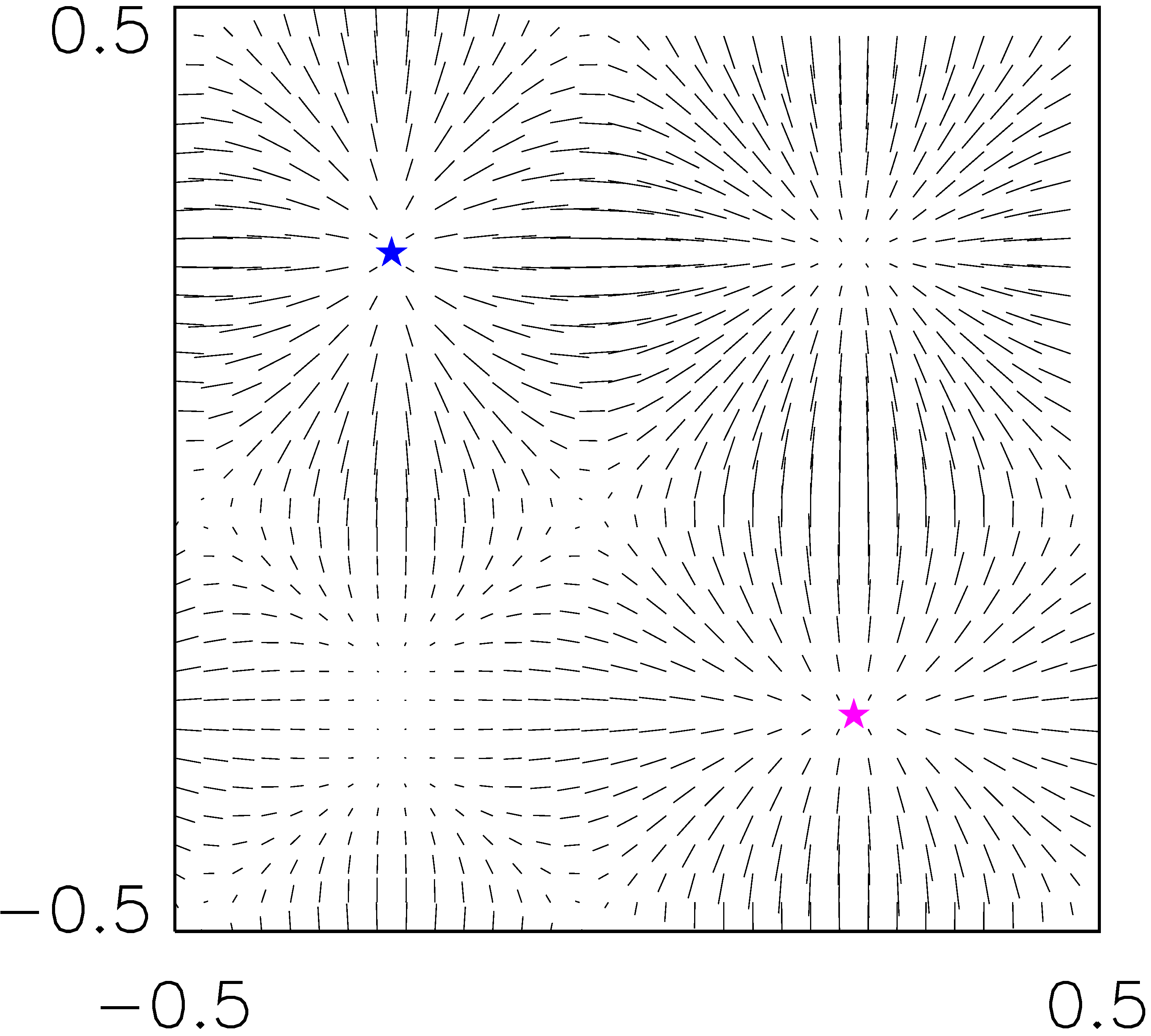
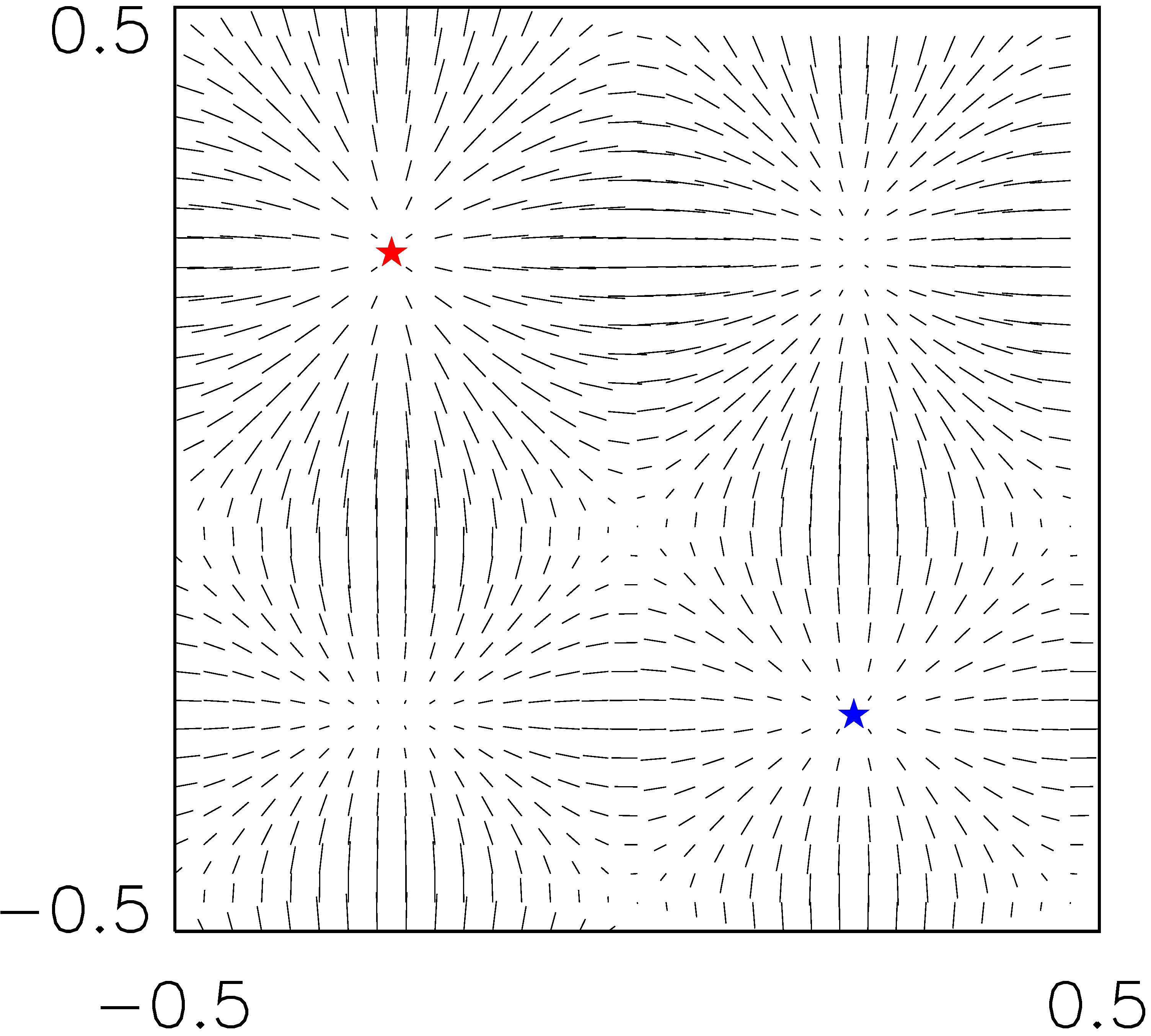
∇u’ на плоскостях, параллельных координатным, проходящих через три модельные «галактики», положение которых показано звездами. Цвет кодирует массы галактик: синий, фиолетовый, красный, в порядке возрастания масс.
Публикации:
Zheligovsky V., Podvigina O., Frisch U. The Monge-Ampère equation: various forms and numerical methods. J. Computational Physics, 229, 2010, 5043-5061 [arxiv.org/abs/0910.1301].