Разложение решения уравнений идеальной магнитогидродинамики в ряд Тейлора по времени может быть использовано для его вычисления.
Доказано, что, если начальные скорость течения жидкости и магнитное поле — аналитические функции пространственных переменных, то решение системы трехмерных уравнений идеальной магнитогидродинамики аналитично по пространственным переменным и времени на некотором временнóм интервале строго положительной длины. С использованием свойства вмороженности магнитного поля построены разложения решения в эйлеровых и лагранжевых координатах в ряды Тейлора по времени. Для их коэффициентов выведены рекуррентные соотношения. Эти результаты положены в основу алгоритмов численного интегрирования рассматриваемых уравнений по времени. Лагранжев алгоритм опробован в расчетах; в решении наблюдается образование структур меньших размерностей. Уже при t≈1.5 использованное пространственное разрешение 2563 гармоник Фурье оказывается недостаточным, и на изоповерхностях появляется численная «рябь».
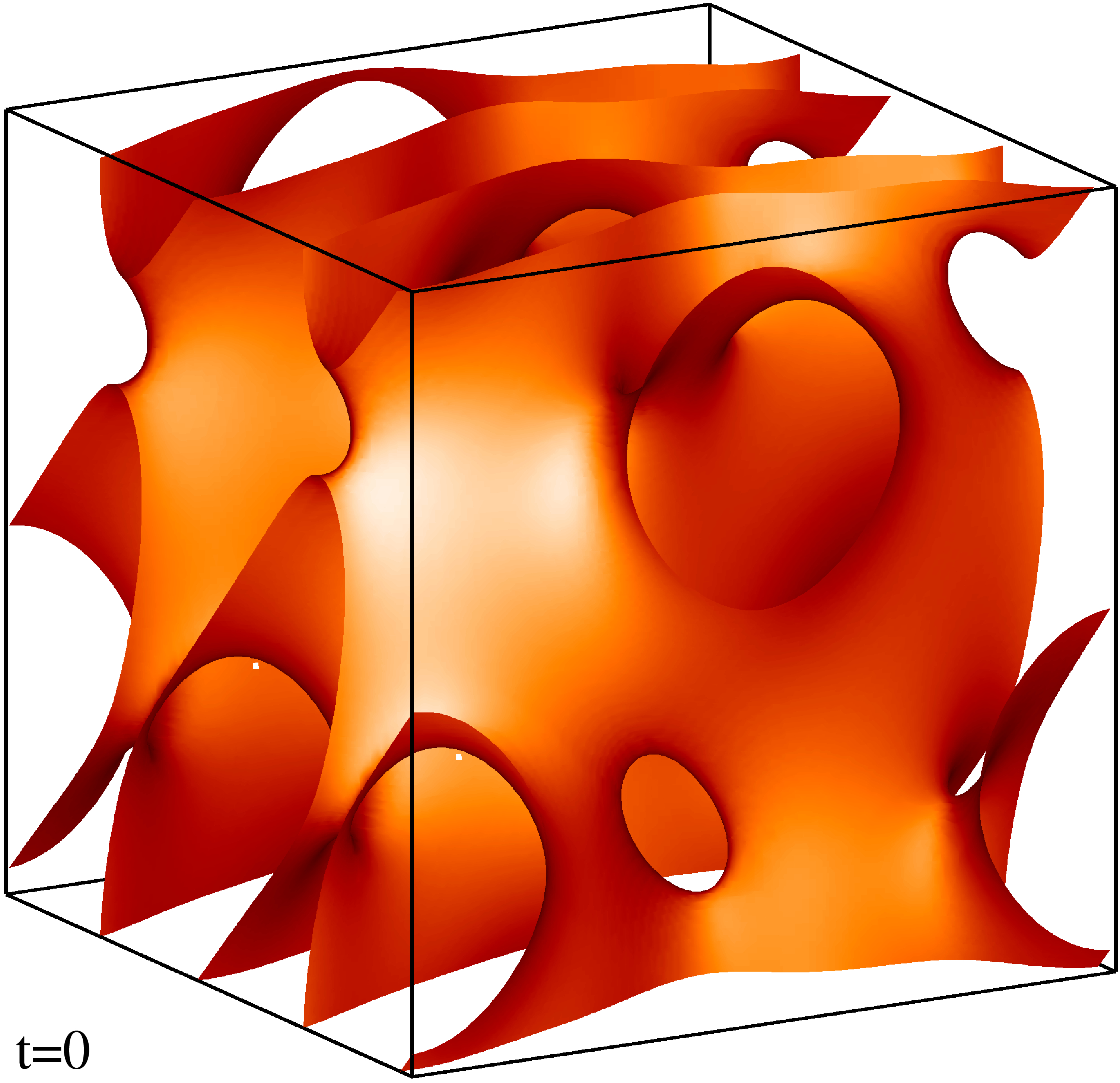
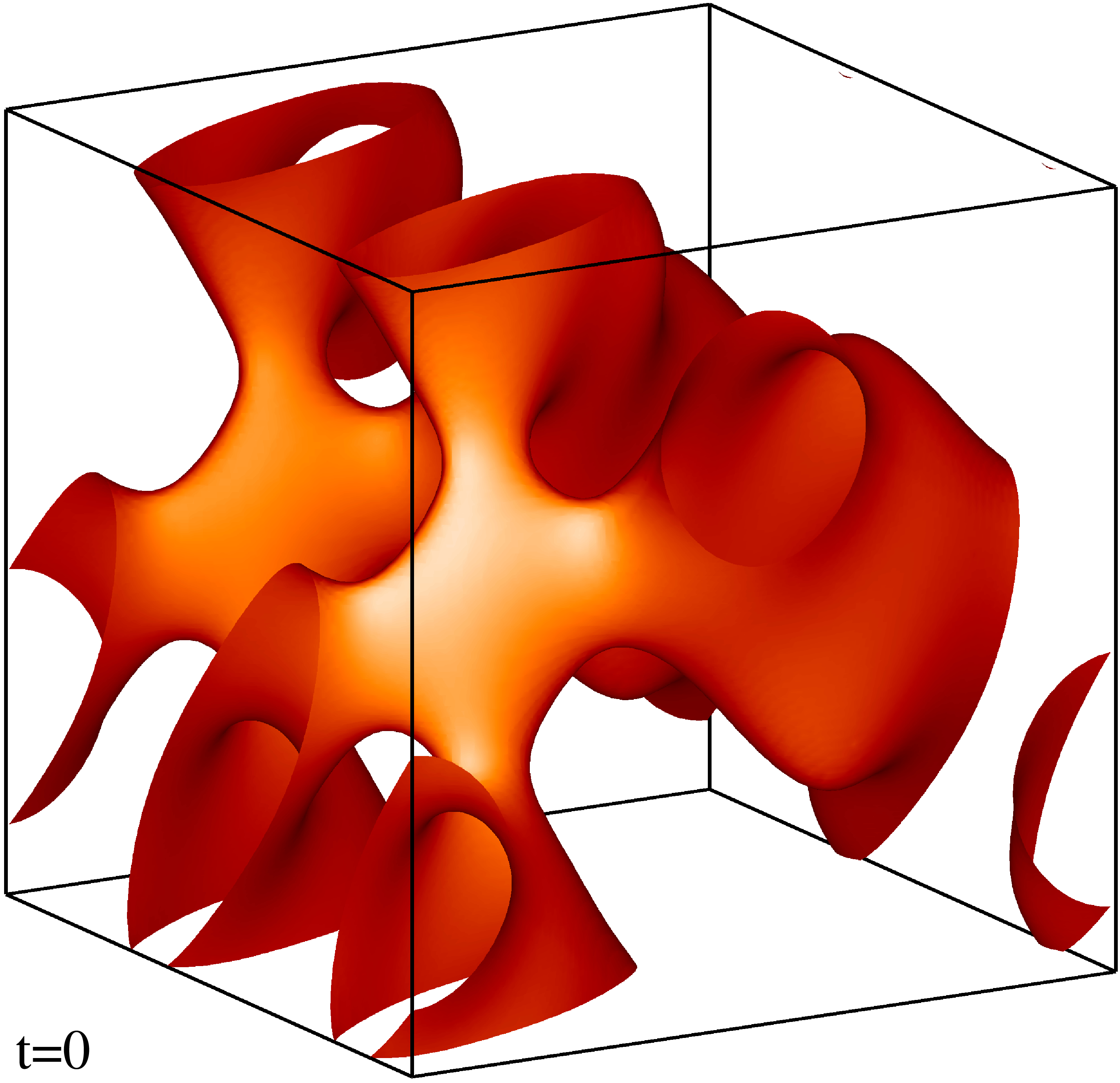
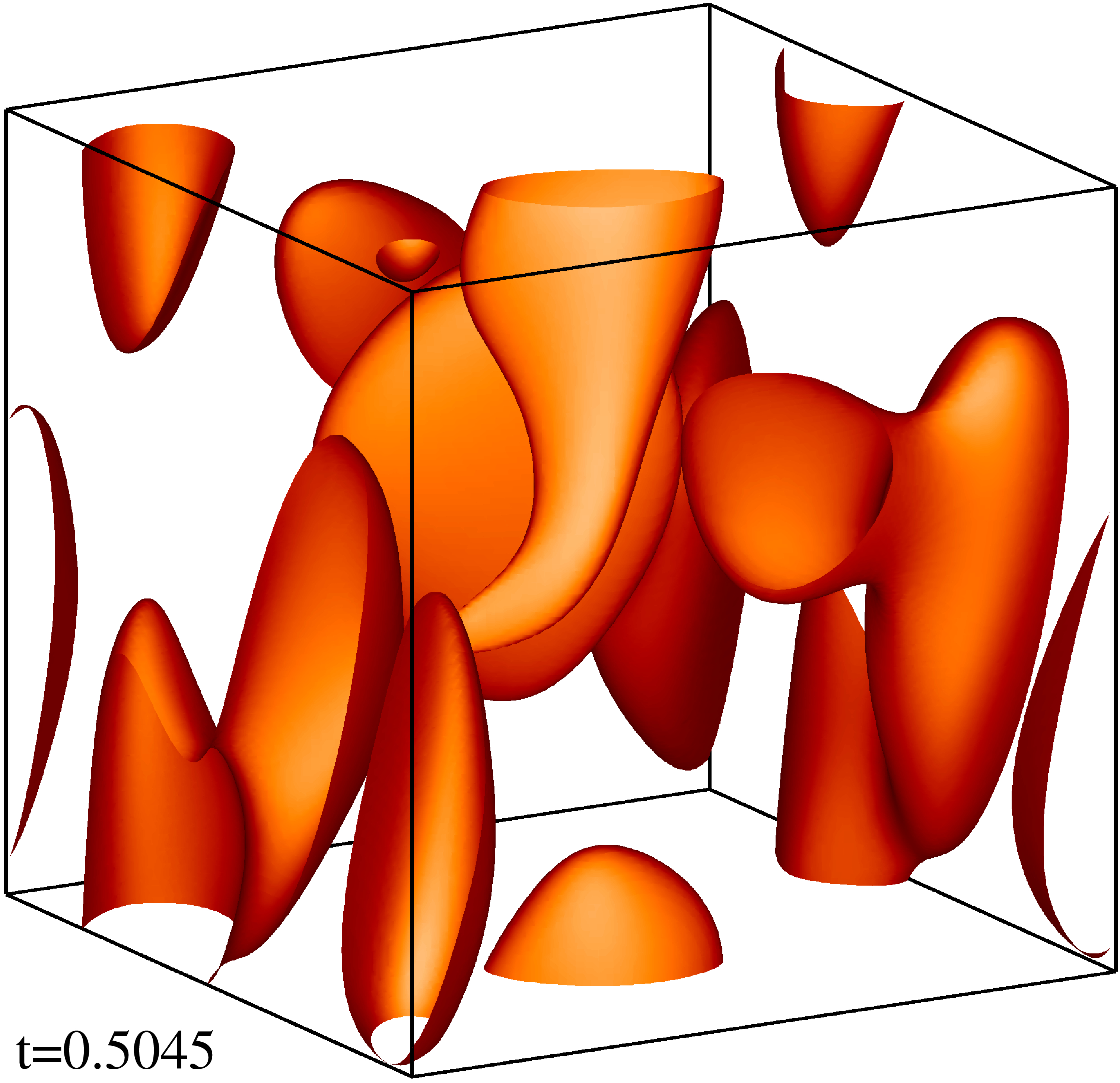
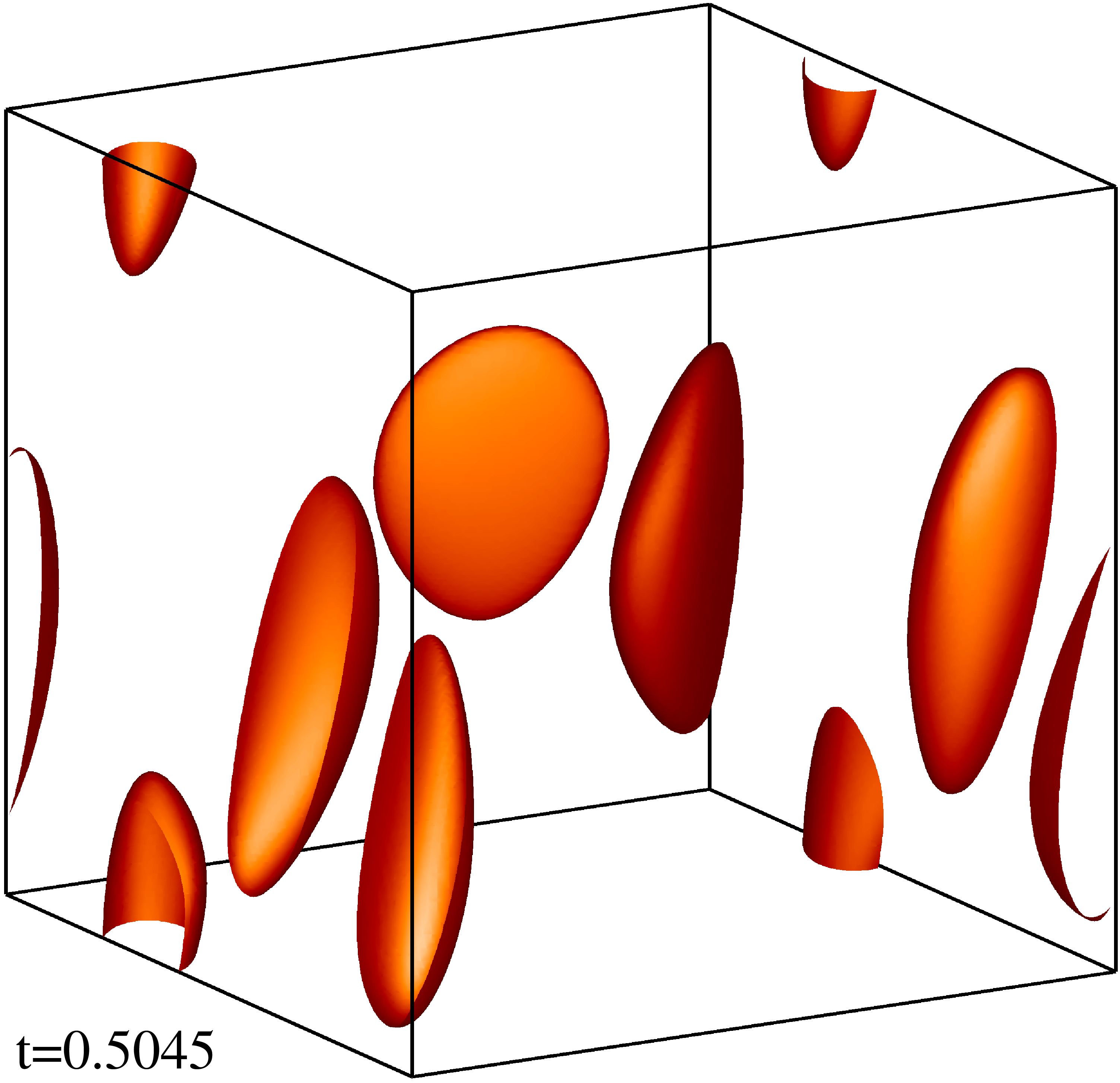
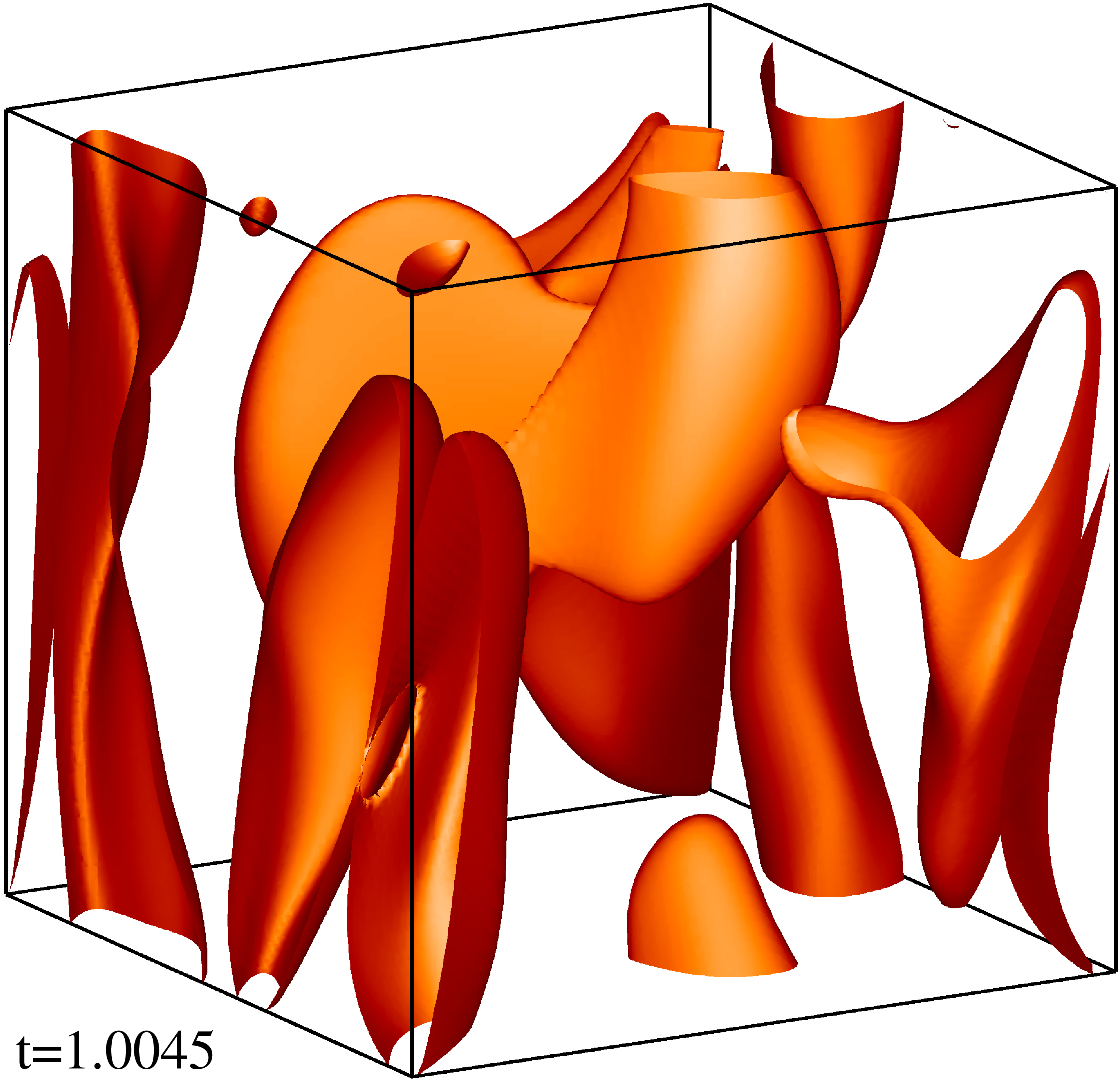
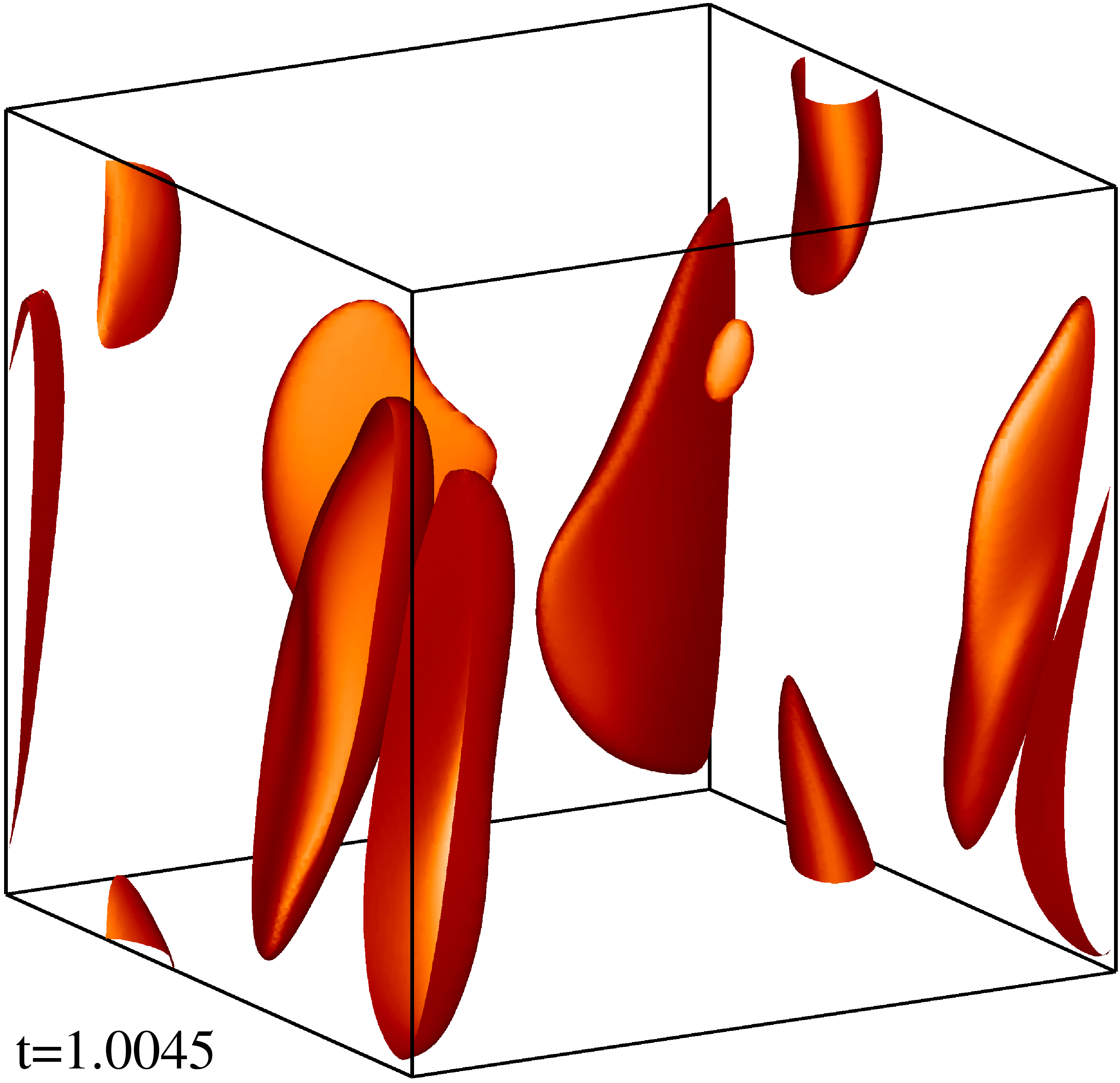
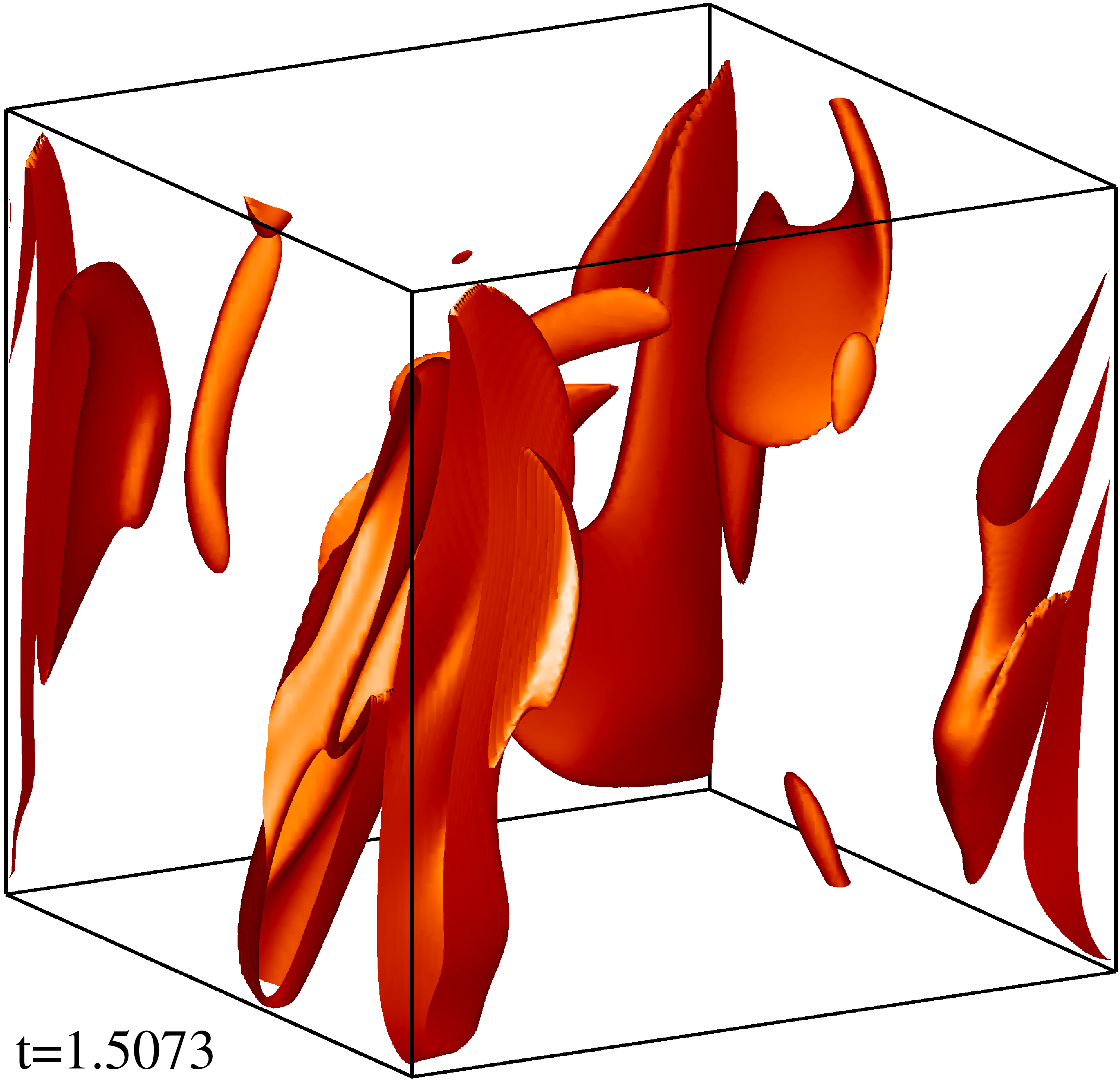
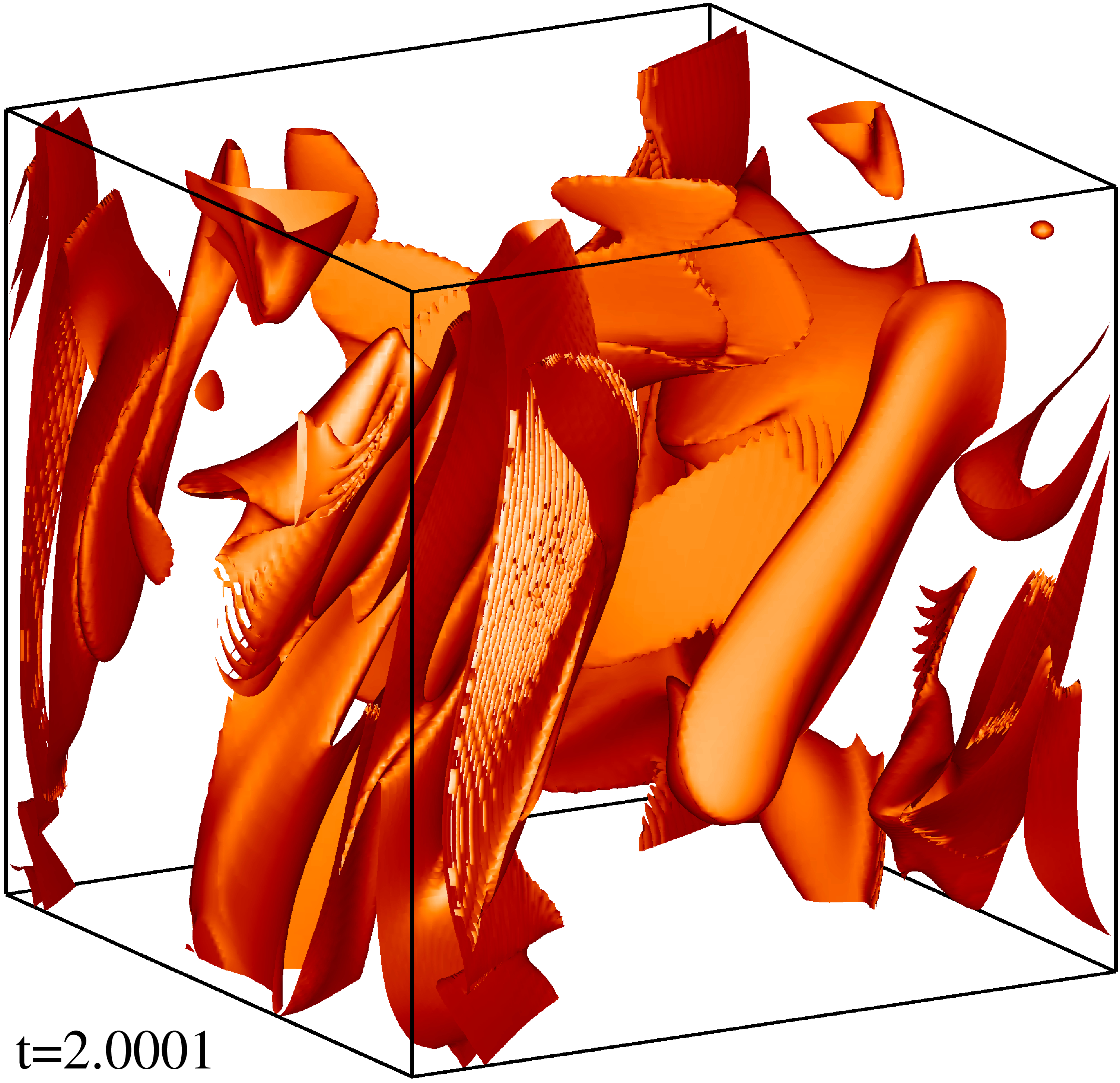
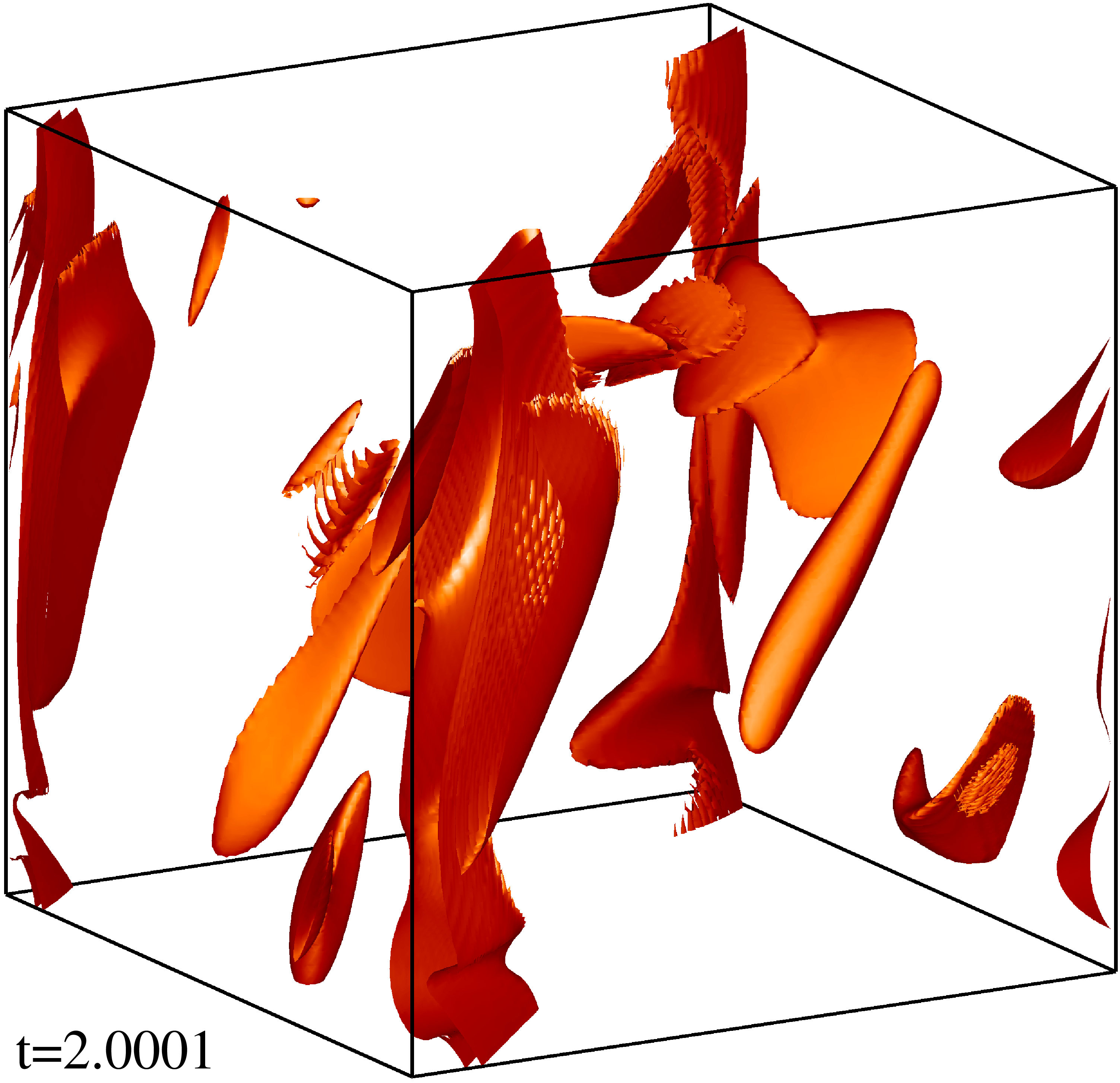
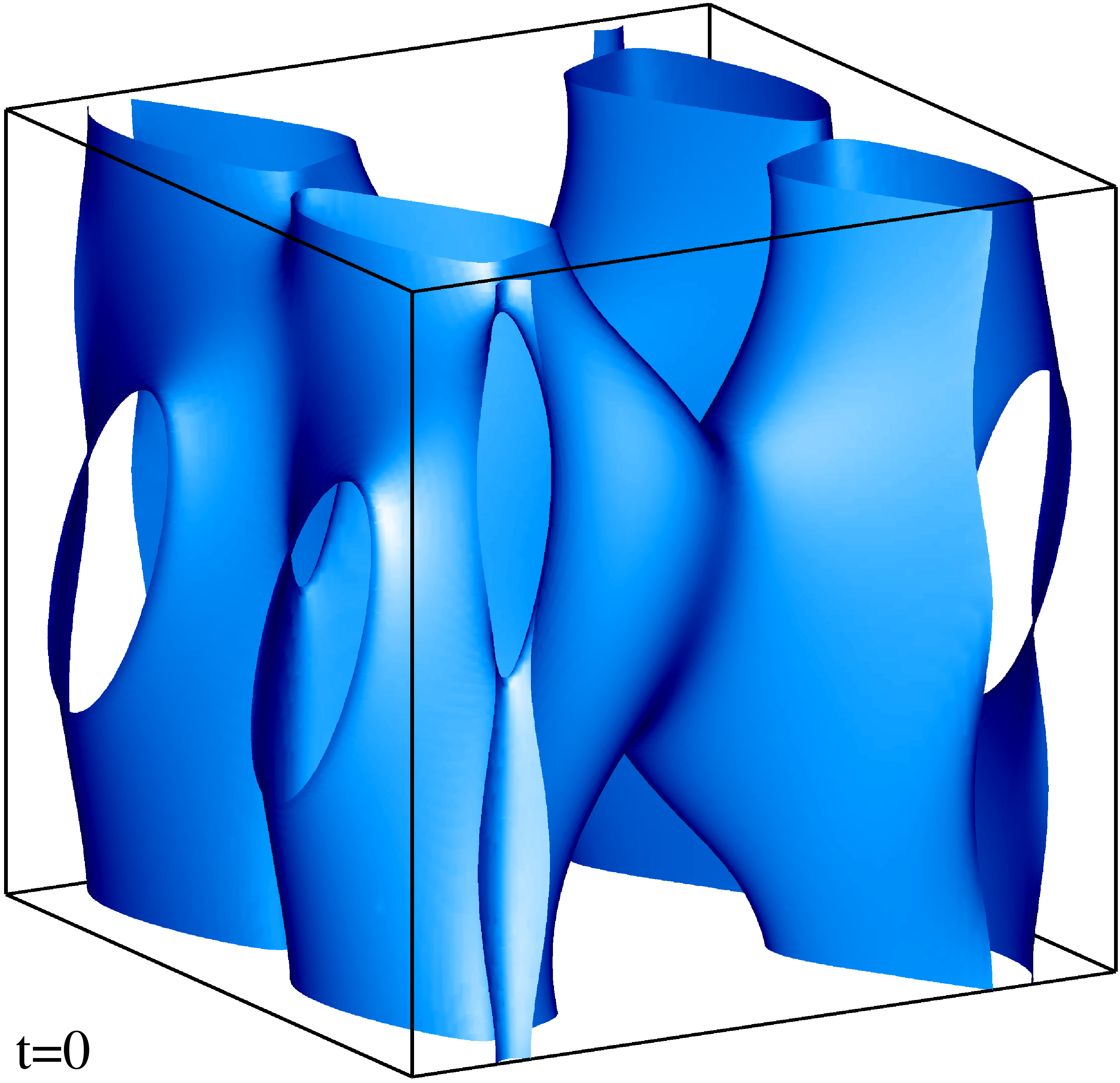
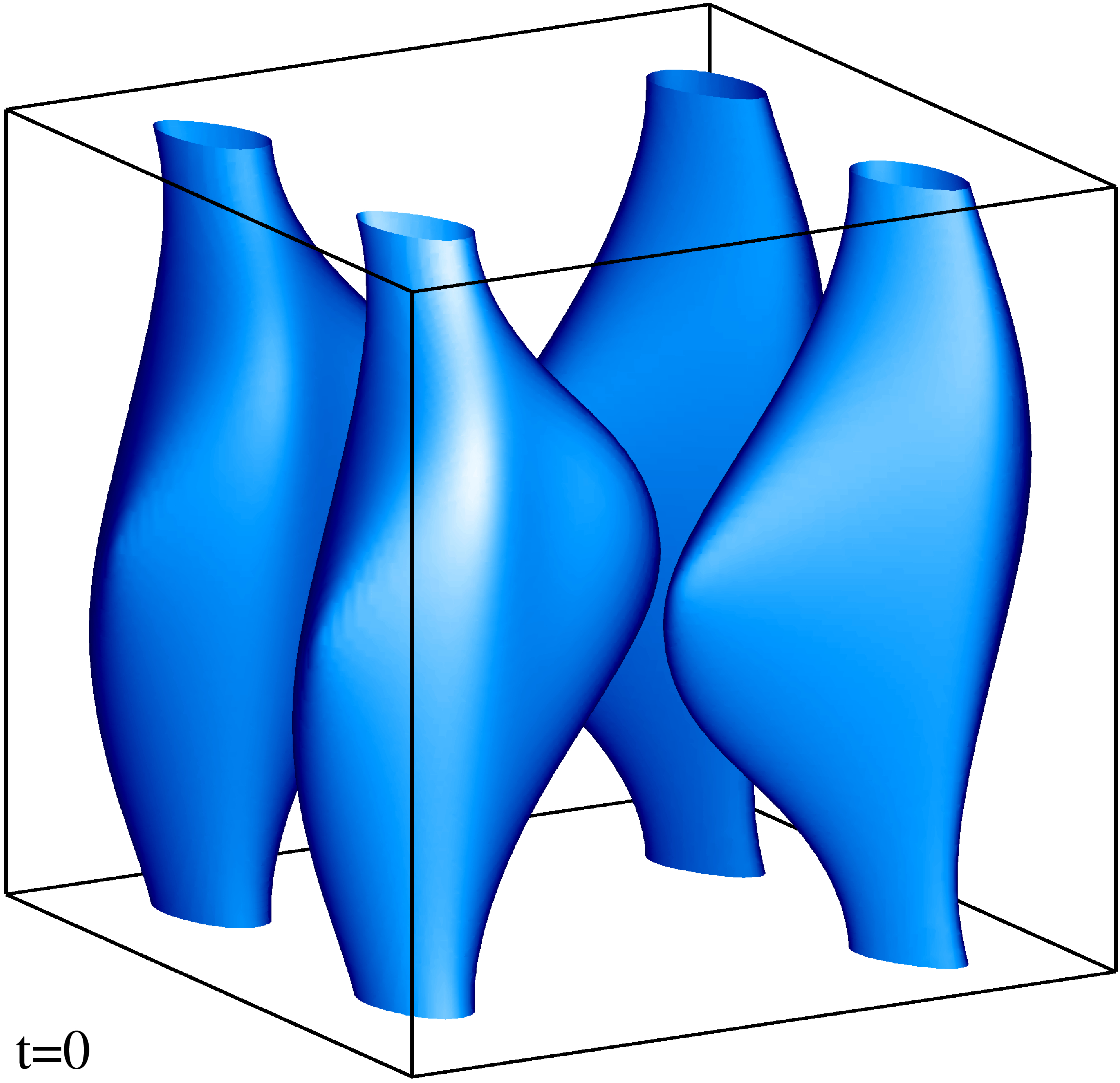
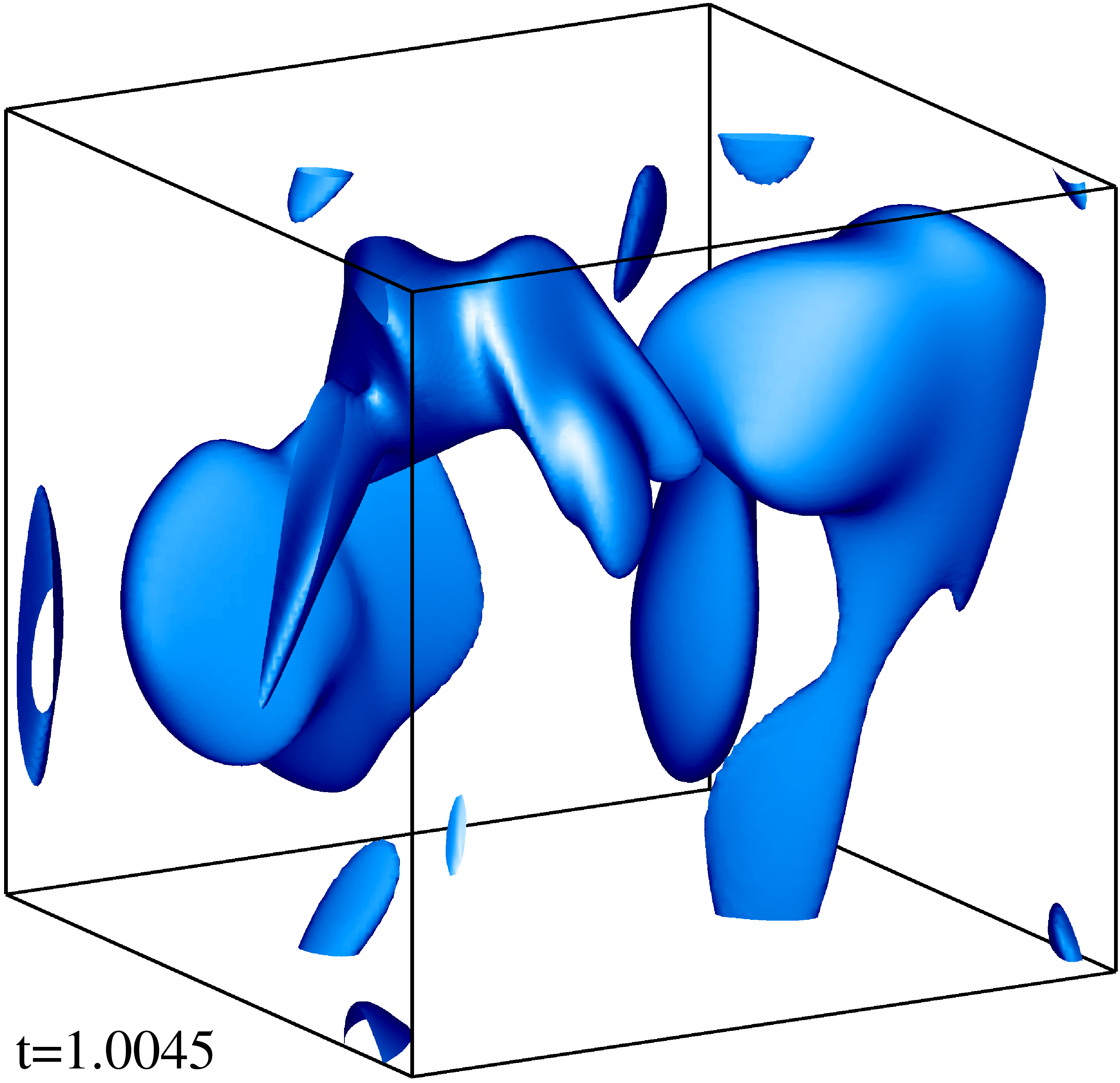
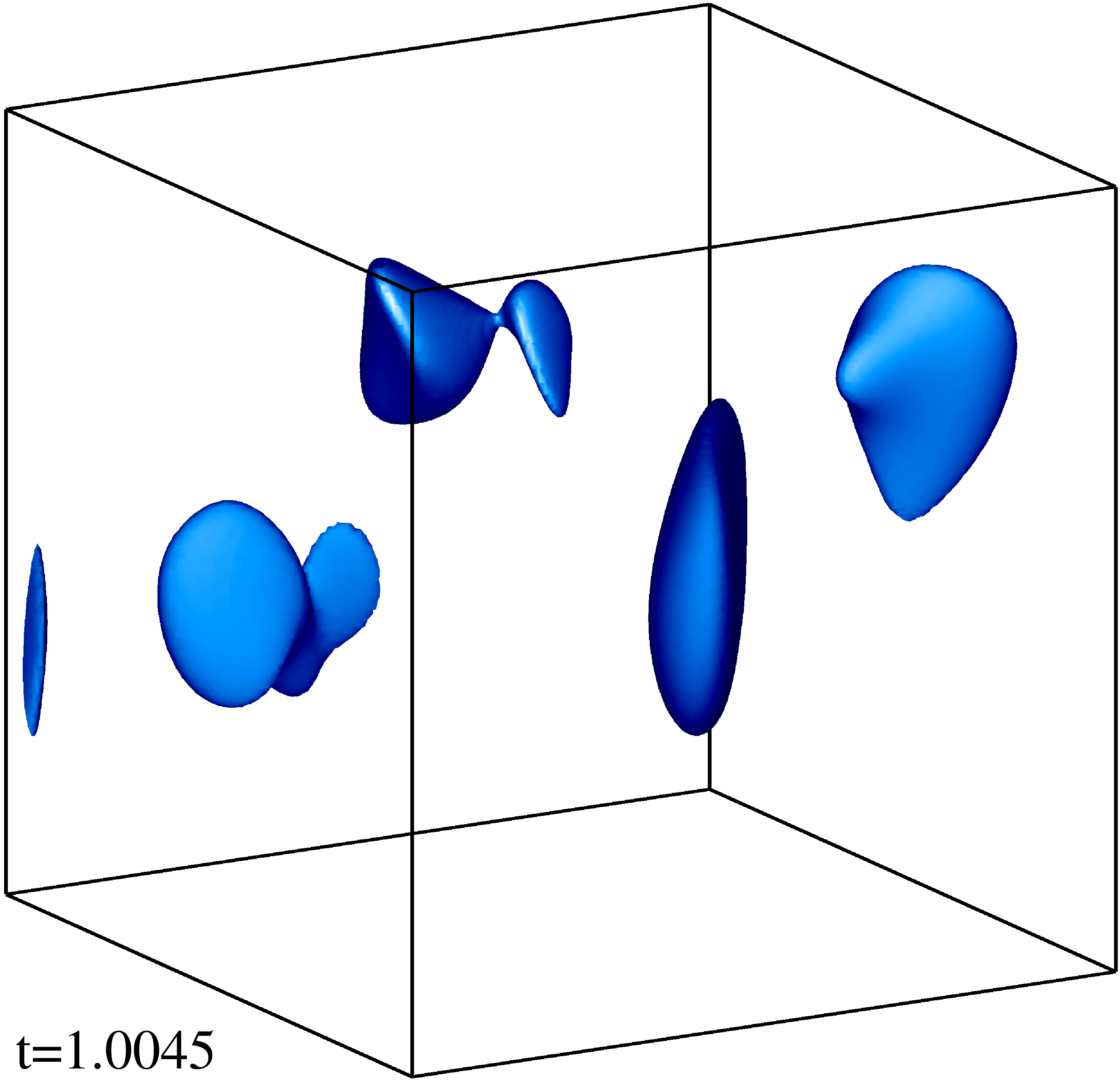
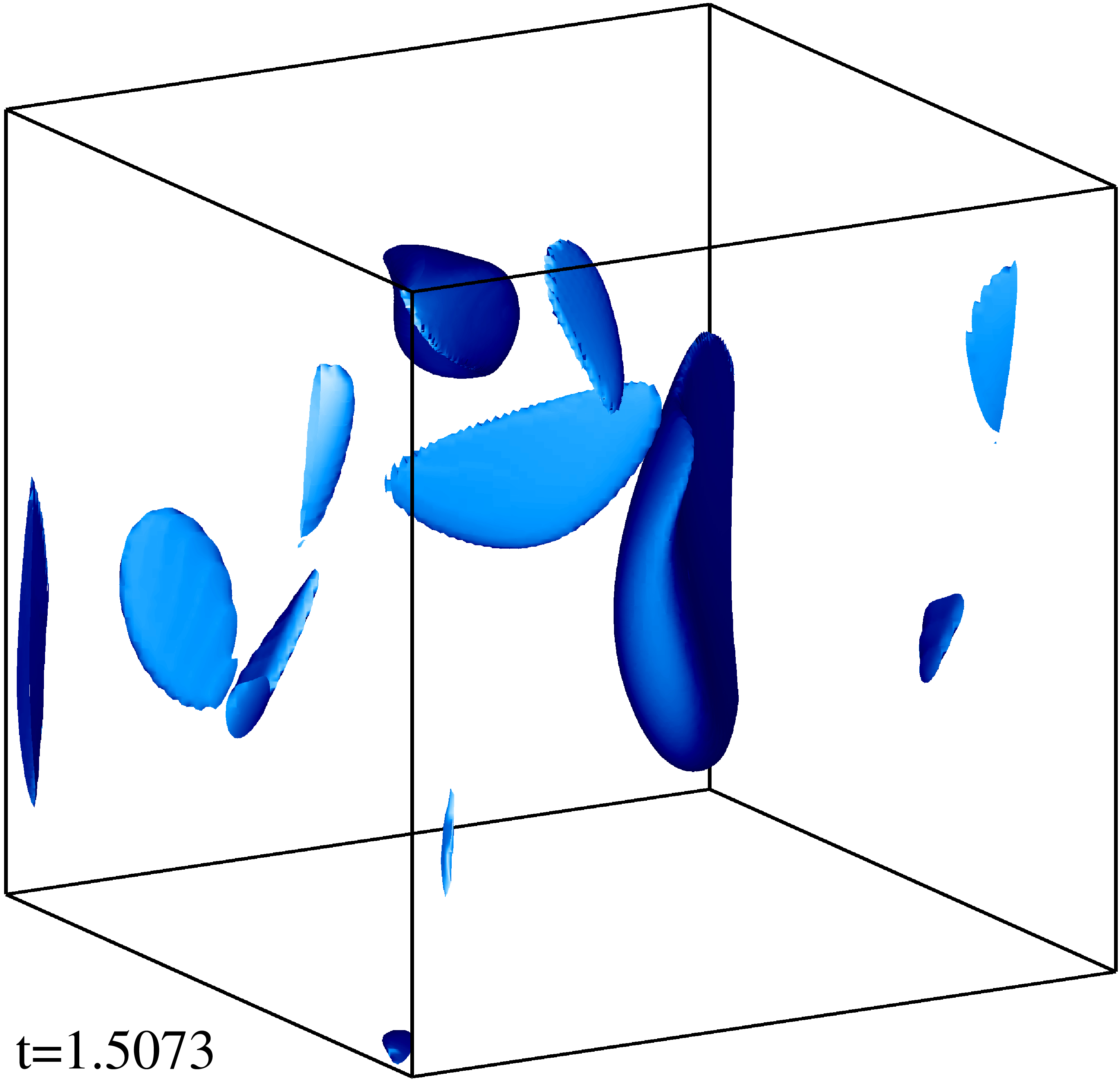
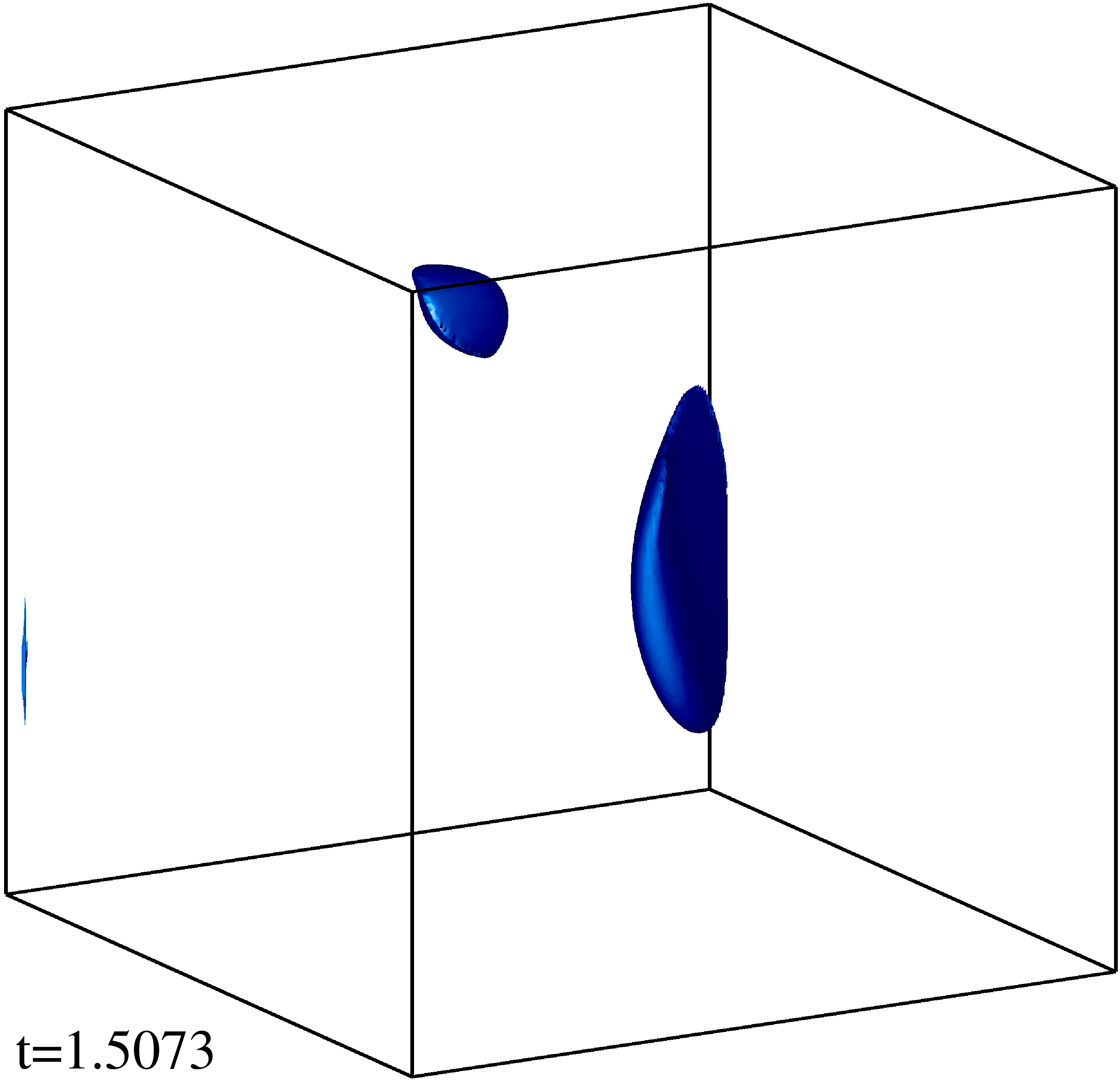
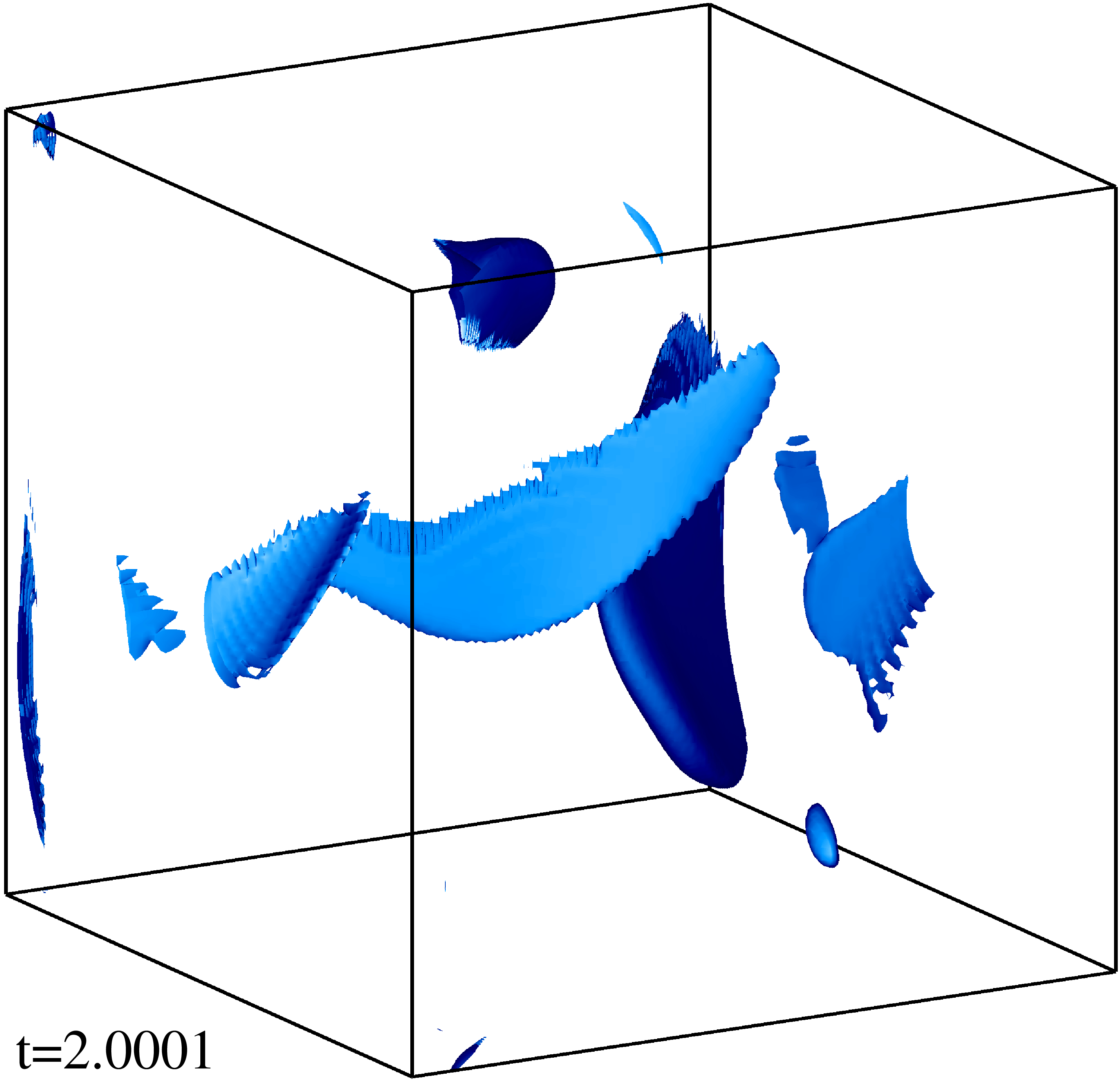
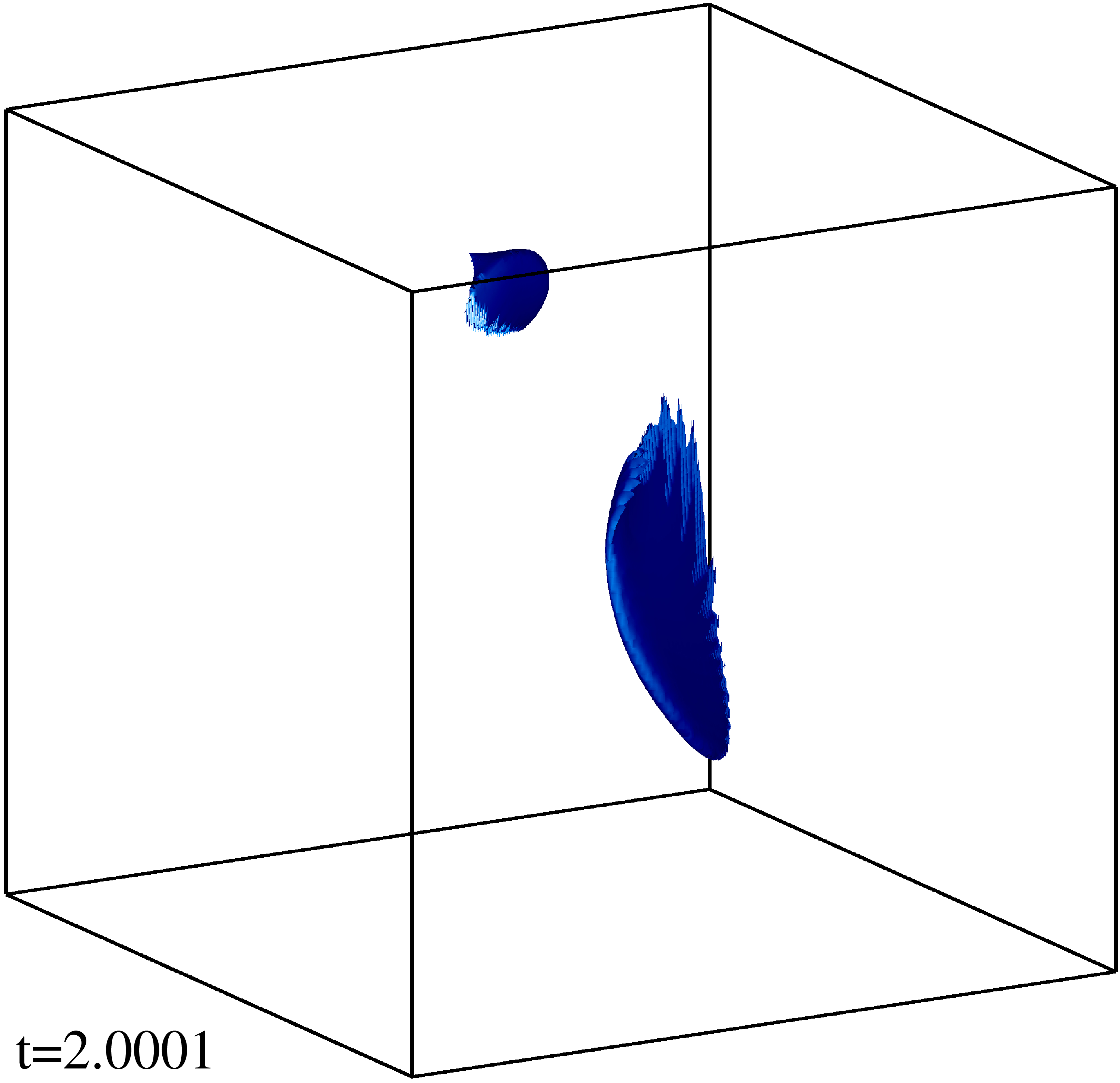
Изоповерхности плотности кинетической энергии течения на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ≈0.5 (точные времена t указаны на рисунке). Изображен один куб периодичности течения.
Изоповерхности плотности магнитной энергии течения на уровне 1/3 (левый столбец) и 1/2 (правый столбец) максимума с шагом по времени ≈0.5 (точные времена t указаны на рисунке). Изображен один куб периодичности течения.
Публикации:
В.А. Желиговский, О.М. Подвигина. Численный алгоритм интегрирования по времени задач идеальной магнитогидродинамики, опирающийся на аналитичность их решений. Физика Земли, №1, 2020.